问题描述

Write an efficient algorithm that searches for a target value in an m x n integer matrix. The matrix has the following properties:

  • Integers in each row are sorted in ascending from left to right.

  • Integers in each column are sorted in ascending from top to bottom.

测试样例

1
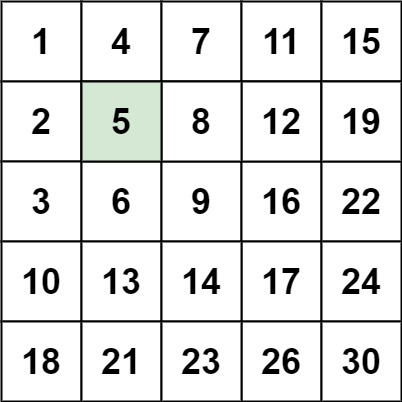
2
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true

1
2
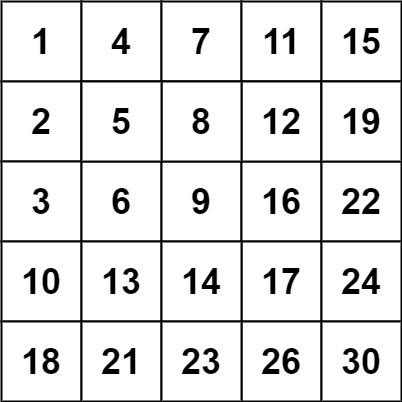
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false

说明

1
2
3
4
5
6
7
m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-10^9 <= matix[i][j] <= 10^9
All the integers in each row are sorted in ascending order.
All the integers in each column are sorted in ascending order.
-10^9 <= target <= 10^9

解题

思路

取最左下方元素为基准 pivot，

  • 若 pivot 值比目标小，则目标在其右侧，横坐标右移一位

  • 若 pivot 值比目标大，则目标在其上侧，纵坐标上移一位

补充：

  1. 时间复杂度 O(logn)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int left = 0, bottom = matrix.length - 1;
        
        while(left < matrix[0].length && bottom >= 0) {
            if(matrix[bottom][left] == target) {
                return true;
            }
            // 在右侧
            else if(matrix[bottom][left] < target) {
                ++left;
            }
            // 在上方
            else {
                --bottom;
            }
        }
        
        // 没找到
        return false;
    }
}