问题描述

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

Integers in each row are sorted from left to right.
The first integer of each row is greater than the last integer of the previous row.

测试样例

1
2
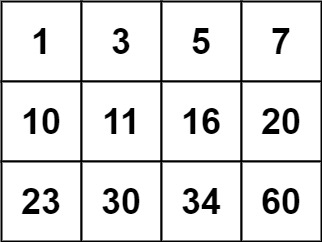
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

1
2
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

说明

1
2
3
4
m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-10^4 <= matrix[i][j], target <= 10^4

解题

思路

首先使用二分法判断目标所在行，然后再使用二分法判断该行中目标所在位置。

补充：

  1. 时间复杂度 O(logn)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int row = locateRaw(matrix, target);
        
        int l = 0, r = matrix[0].length - 1;
        
        while(l <= r) {
            int mid = l + (r - l) / 2;
            
            if(matrix[row][mid] == target) {
                return true;
            }
            // 在左侧
            else if(matrix[row][mid] > target) {
                r = mid - 1;
            }
            // 在右侧
            else {
                l = mid + 1;
            }
        }
        
        return false;
    }
    
    /**
     * 定位目标所在行
     */
    public int locateRaw(int[][] matrix, int target) {
        int top = 0, bottom = matrix.length - 1;
        
        while(top < bottom) {
            int mid = top + (bottom - top) / 2;
            
            // 在 mid 行中
            if(matrix[mid][0] <= target && target <= matrix[mid][matrix[mid].length - 1]) {
                return mid;
            }
            // 在 mid 行之下
            else if(matrix[mid][0] < target) {
                top = mid + 1;
            }
            // 在 mid 行之上
            else {
                bottom = mid - 1;
            }
        }
        return top;
    }
}