MTL 算法公式

传统 MTL 算法的典型公式如下：

min⁡W=[w1w2…wM]∑m=1ML(Xm,ym,wm)+λReg⁡(W)\min _{\mathbf{W}=\left[\mathbf{w}^{1} \mathbf{w}^{2} \ldots \mathbf{w}^{M}\right]} \sum_{m=1}^{M} L\left(\mathbf{X}^{m}, \mathbf{y}^{m}, \mathbf{w}^{m}\right)+\lambda \operatorname{Reg}(\mathbf{W})

其中，

  • Xm∈RNm×D\mathbf{X}^{m} \in \R^{N_m \times D} 表示第 mm 个任务的输入矩阵
  • ym∈RNm×1\mathbf{y}^{m} \in \R^{N_m \times 1} 表示第 mm 个任务对应的输出向量
  • wm∈RD×1\mathbf{w}^{m} \in \R^{D \times 1} 表示第 mm 个任务的权重向量
  • NmN_m 表示第 mm 个任务的样本数
  • DD 表示输入矩阵的特征数
  • mm 表示任务数。

上式由两项组成，

  • 数据保真项，用于计算目标预测与地面真实目标的匹配程度；
  • 正则化项，对权重矩阵W进行正则化以获取不同学习任务之间的关系；

不同的 MTL 数据保真项

MTL 问题分为三种特殊情况，

  • 多输入单输出（MISO）
  • 单输入多输出（SIMO）
  • 多输入多输出（MIMO）

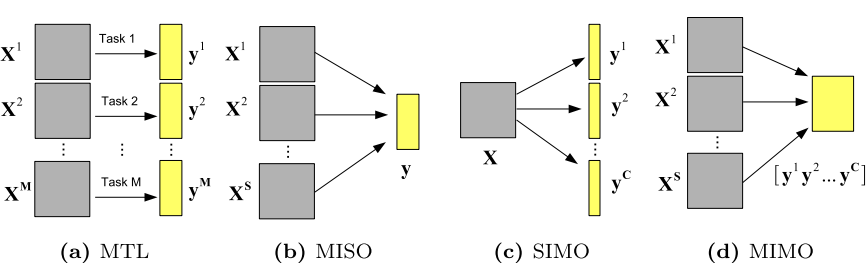
MTL 对比

X：输入数据； Y：目标输出；

(a) 多任务学习的一般形式
(b) 多输入单输出（MISO），多组输入映射到同一组输出目标
© 单输入多输出（SIMO），一组输入被映射到多组输出目标
(d) 多输入多输出（MIMO），多组输入被映射到相同的多组输出目标。

多输入单输出（MISO）

有多个数据源，并且所有数据源都映射到相同的目标 yy。 此处的任务定义为一个数据源映射到该共同目标 yy 的预测。

对于回归任务，数据保真度项的均方损失公式为：

L(X,y,W)=∑sS∥Xsws−y∥F2L(\mathbf{X}, \mathbf{y}, \mathbf{W})=\sum_{s}^{S}\left\|\mathbf{X}^{s} \mathbf{w}^{s}-\mathbf{y}\right\|_{F}^{2}

其中，

  • X={X1,X2,...,XS}\mathbf{X} = \{\mathbf{X}^1, \mathbf{X}^2,...,\mathbf{X}^S\} 表示多源（视图或多模态）数据集
  • Xs∈RN×D\mathbf{X}^s \in \R^{N \times D} 表示第 ss 个数据源
  • y∈RN×1\mathbf{y} \in \R^{N \times 1} 表示输出特征向量
  • W=[w1w2⋅⋅⋅wS]∈RD×S\mathbf{W} = [\mathbf{w}^1 \mathbf{w}^2 ··· \mathbf{w}^S] \in \R^{D \times S} 表示权重矩阵
  • NN 表示样本数
  • SS 表示数据源数
  • DD 表示每个数据源中的特征数。

对于分类任务，数据保真度项可以采用 logistic 或 hinge 损失函数：

L(X,y,W)=∑sS∑jNlog⁡(1+exp⁡(−y^jsyj))L(X,y,W)=∑sS∑jNmax⁡(0,1−y^jsyj)\begin{array}{c} L(\mathbf{X}, \mathbf{y}, \mathbf{W})=\sum_{s}^{S} \sum_{j}^{N} \log \left(1+\exp \left(-\hat{y}_{j}^{s} y_{j}\right)\right) \\ L(\mathbf{X}, \mathbf{y}, \mathbf{W})=\sum_{s}^{S} \sum_{j}^{N} \max \left(0,1-\hat{y}_{j}^{s} y_{j}\right) \end{array}

其中，

  • y^js=xjSws\hat{y}_{j}^{s} = \mathbf{x}^S_j \mathbf{w}^s 表示对第 ss 个数据源的第 jj 个样本的预测（xjs\mathbf{x}^s_j）
  • yj∈{−1,1}y_j \in \{-1,1\} 表示对应的 ground truth 标签

单输入多输出（SIMO）

只有一个输入（或所有任务共享相同的输入），用于预测不同类型的输出目标。 此处的任务定义为输入矩阵 X\mathbf{X} 映射到目标矢量的预测。

数据保真项的均方损失函数为：

L(X,Y,W)=∑cC∥Xwc−yc∥F2=∥XW−Y∥F2L(\mathbf{X}, \mathbf{Y}, \mathbf{W})=\sum_{c}^{C}\left\|\mathbf{X} \mathbf{w}^{c}-\mathbf{y}^{c}\right\|_{F}^{2} = \|\mathbf{X} \mathbf{W} - \mathbf{Y}\|_{F}^{2}

其中，

  • X∈RN×D\mathbf{X} \in \R^{N \times D} 表示输入特征矩阵
  • Y={y1...yS}\mathbf{Y} = \{\mathbf{y}^1...\mathbf{y}^S\} 表示输出目标矩阵
  • W=[w1w2⋅⋅⋅wC]∈RD×C\mathbf{W} = [\mathbf{w}^1 \mathbf{w}^2 ··· \mathbf{w}^{C}] \in \R^{D \times C} 表示相应的权重矩阵

logistic 和 hinge 损失函数与多输入单输出类似，只需将数据源数 SS 替换成目标数。

多输入多输出（MIMO）

多个输入源可用于预测多个输出目标。 此处的任务定义为一个输入源映射到单个目标的的预测。

数据保真度项的均方损失函数为：

L(X,Y,W)=∑sS∑cC∥Xsws,c−yc∥F2=∑sS∥XsWs−Y∥F2L(\mathbf{X}, \mathbf{Y}, \mathbf{W})=\sum_{s}^{S}\sum_{c}^{C}\left\|\mathbf{X}^{s} \mathbf{w}^{s,c}-\mathbf{y}^{c}\right\|_{F}^{2} = \sum_{s}^{S}\left\|\mathbf{X}^{s} \mathbf{W}^{s} - \mathbf{Y}\right\|_{F}^{2}

其中，

  • X={X1,X2,...,XS}\mathbf{X} = \{\mathbf{X}^1,\mathbf{X}^2,...,\mathbf{X}^S\} 表示多源（视图或多模态）数据集
  • Y={y1...yS}\mathbf{Y} = \{\mathbf{y}^1...\mathbf{y}^S\} 表示输出目标矩阵
  • W=[w1w2⋅⋅⋅wC]∈RD×C\mathbf{W} = [\mathbf{w}^1 \mathbf{w}^2 ··· \mathbf{w}^{C}] \in \R^{D \times C} 表示所有权重矩阵的集合
  • Ws=[ws,1ws,2⋅⋅⋅ws,C]∈RD×C\mathbf{W}^{s} = [\mathbf{w}^{s, 1} \mathbf{w}^{s, 2} ··· \mathbf{w}^{s,C}] \in \R^{D \times C} 表示第 ss 个模态数据 Xs\mathbf{X}^{s} 的权重矩阵

logistic 和 hinge 损失函数与多输入单输出类似。

在某些应用中，多源数据可以被合并为单个输入数据，这将这个问题简化为SIMO。

不同的 MTL 权重矩阵 W\mathbf{W} 正则化

具有 lasso 约束的 MTL

通过对 W\mathbf{W} 进行 l1-norm\mathcal{l}_1 \text{-norm} 正则化，给出具有Lasso约束的的多任务学习：

min⁡W∑m=1ML(Xm,ym,wm)+λ∥W∥1\min _{\mathbf{W}} \sum_{m=1}^{M} L\left(\mathbf{X}^{m}, \mathbf{y}^{m}, \mathbf{w}^{m}\right)+\lambda\|\mathbf{W}\|_{1}

其中，

  • W=[w1w2⋅⋅⋅wM]\mathbf{W} = [\mathbf{w}^1 \mathbf{w}^2 ··· \mathbf{w}^{M}]
  • λλ 是控制稀疏性的正则化参数

具有组稀疏约束的 MTL

  1. l2,1-norm\mathcal{l}_{2,1}\text{-norm}
    为了从多个相关任务中提取任务相关性信息，需要约束所有模型共享一组相同的特征。 通过解决以下 l2,1-norm\mathcal{l}_{2,1}\text{-norm} 正则化实现：

    min⁡W∑m=1ML(Xm,ym,wm)+λ∥W∥2,1\min _{\mathbf{W}} \sum_{m=1}^{M} L\left(\mathbf{X}^{m}, \mathbf{y}^{m}, \mathbf{w}^{m}\right)+\lambda\|\mathbf{W}\|_{2, 1}

    其中，

    • ∥W∥2,1=∑i=1D∥wi∥2\|\mathbf{W}\|_{2, 1} = \sum^{D}_{i=1}{\|\mathbf{w}_i\|_2}
    • wi∈R1×M\mathbf{w}_i \in \R^{1 \times M} 表示 W\mathbf{W} 中的第 ii 行

  2. lp,q-norm\mathcal{l}_{p,q}\text{-norm}
    可以将 l2,1-norm\mathcal{l}_{2,1}\text{-norm} 推广为 lp,q-norm\mathcal{l}_{p,q}\text{-norm} 正则化来选择特征：

    min⁡W∑m=1ML(Xm,ym,wm)+λ∥W∥p,q\min _{\mathbf{W}} \sum_{m=1}^{M} L\left(\mathbf{X}^{m}, \mathbf{y}^{m}, \mathbf{w}^{m}\right)+\lambda\|\mathbf{W}\|_{p, q}

    其中，

    • ∥W∥p,q=∥[∥w1∥p⋯∥wi∥p⋯∥wD∥p]∥q\|\mathbf{W}\|_{p, q} = \left\|\left[\|\mathbf{w}_1\|_p \cdots \|\mathbf{w}_i\|_p \cdots \|\mathbf{w}_D\|_p\right]\right\|_q
    • 若 $ p > 1, q \ge 1$ 则为凸函数

  3. 有上界的 lp,1-norm\mathcal{l}_{p,1}\text{-norm}
    wi\mathbf{w}_i 的 lp,1-norm\mathcal{l}_{p,1} \text{-norm} 上界：

    min⁡W∑m=1ML(Xm,ym,wm)+λ∑i=1Dmin⁡(∥wi∥p,θ)\min _{\mathbf{W}} \sum_{m=1}^{M} L\left(\mathbf{X}^{m}, \mathbf{y}^{m}, \mathbf{w}^{m}\right)+\lambda \sum_{i=1}^{D} \min(\|\mathbf{w}_i\|_p, \theta)

    其中，

    • θ\theta 是阈值
    • lp,1-norm\mathcal{l}_{p,1}\text{-norm} 算法使 W\mathbf{W} 中小于 θ\theta 的行最小化，从而提高解的稀疏性。

  4. 多级 lasso
    将权重矩阵分解为几个组成部分，并对它们施加不同的正则化：

    min⁡w~,θ∑m=1ML(Xm,ym,wm)+λ1∥θ∥1+λ2∥W~∥1,s.t.W=diag⁡(θ)W~\min _{\tilde{\mathbf{w}}, \boldsymbol{\theta}} \sum_{m=1}^{M} L\left(\mathbf{X}^{m}, \mathbf{y}^{m}, \mathbf{w}^{m}\right)+\lambda_{1}\|\boldsymbol{\theta}\|_{1}+\lambda_{2}\|\tilde{\mathbf{W}}\|_{1}, s . t . \mathbf{W}=\operatorname{diag}(\boldsymbol{\theta}) \tilde{\mathbf{W}}

    其中，

    • θ∈RD×1\theta \in \R^{D \times 1} 是控制特征级组稀疏度的非负系数矢量

  5. Structured group lasso
    pass

  6. 时序组 Lasso
    在学习任务涉及时间的情况下，在 WW 上添加时间平滑度约束以确保相邻时间点的权向量一致。

    带有时间平滑项的 MTL 为：

    min⁡W∑m=1ML(Xm,ym,wm)+λ1∥W∥F2+λ2∑m=1M−1∥wm−wm+1∥22\min _{\mathbf{W}} \sum_{m=1}^{M} L\left(\mathbf{X}^{m}, \mathbf{y}^{m}, \mathbf{w}^{m}\right)+\lambda_{1}\|\mathbf{W}\|_{F}^{2}+\lambda_{2} \sum_{m=1}^{M-1}\left\|\mathbf{w}^{m}-\mathbf{w}^{m+1}\right\|_{2}^{2}

具有低秩约束的 MTL

约束来自不同任务的预测模型以共享低维子空间，即 W\mathbf{W} 是低秩的。可以通过秩最小化问题的替代近似值来实现：

min⁡W∑m=1ML(Xm,ym,wm)+λ∥W∥∗\min _{\mathbf{W}} \sum_{m=1}^{M} L\left(\mathbf{X}^{m}, \mathbf{y}^{m}, \mathbf{w}^{m}\right)+\lambda\|\mathbf{W}\|_{*}

其中，

  • ∥⋅∥∗\|\cdot\|_{*} 表示迹范数（核范数），即奇异值之和 ∥W∥∗=∑i=1min⁡(M,D)σi(W)\|\mathbf{W}\|_{*} = \sum_{i=1}^{\min(M, D)}{\sigma_i(\mathbf{W})}

不相关任务的 MTL

可以利用不相关的任务组来改善某些任务的学习。

即使其他任务（例如，辅助任务）与主要任务不相关，仍然可能对主要任务有益。

具有图拉普拉斯正则化的 MTL

可以利用样本之间的关系进行图级别的正则化。

具体来说，我们可以引入图拉普拉斯正则化来保留样本之间的局部拓扑关系，即，使用权重矩阵 W\mathbf W 作变换后保留的样本局部结构信息：

∑i,jNsij∥xiW−xjW∥22=tr⁡(W⊤X⊤LXW)\sum_{i, j}^{N} s_{i j}\left\|\mathbf{x}_{i} \mathbf{W}-\mathbf{x}_{j} \mathbf{W}\right\|_{2}^{2}=\operatorname{tr}\left(\mathbf{W}^{\top} \mathbf{X}^{\top} \mathbf{L} \mathbf{X} \mathbf{W}\right)

其中，

  • L=D−S∈RN×N\mathbf{L} = \mathbf{D} - \mathbf{S} \in \R^{N \times N} 表示拉普拉斯矩阵
  • S=[sij]∈RN×N\mathbf{S} = [s_{ij}] \in \R^{N \times N} 表示每对采样点 xix_i 和 xjx_j 之间的相似矩阵
  • D∈RN×N\mathbf{D} \in \R^{N \times N} 是对角矩阵，其对角线元素定义为 dii=∑jsijd_{ii} = \sum_{j}{s_{ij}}

MTL 关于分解后权重矩阵 W\mathbf{W} 的不同正则化器

将权重矩阵 WW 分解成两个或多个矩阵的和/和的乘积。

在 MTL 脏模型中，权重矩阵被分解为两个矩阵的总和（即 W=P+Q\mathbf{W} = \mathbf{P} + \mathbf{Q}），每个矩阵具有不同的约束条件，以对任务之间的关系进行建模。 在

通常，权重矩阵 WW 可以分解为：

W=P+BA\mathbf{W} = \mathbf{P} + \mathbf{BA}

其中，

  • P\mathbf{P} 表示原始特征空间中的系数矩阵
  • A\mathbf{A} 表示变换特征空间中的系数矩阵
  • B\mathbf{B} 表示变换矩阵

MTL with W=P+Q\mathbf{W} = \mathbf{P} + \mathbf{Q}

  1. 脏方法
    在实际应用中，多个预测模型可能并不具有相同的结构，对于这种情况，简单的使用 l1/lq-norm\mathcal{l}_1 / \mathcal{l}_q \text{-norm} 正则化处理可能是无效的。可以通过将 W\mathbf{W} 分解为两个分量 P\mathbf{P} 和 Q\mathbf{Q} 来解决脏多任务的最小二乘问题：

    min⁡P,Q∑m=1ML(Xm,ym,(pm+qm))+λ1∥P∥1,∞+λ2∥Q∥1\min _{\mathbf{P}, \mathbf{Q}} \sum_{m=1}^{M} L\left(\mathbf{X}^{m}, \mathbf{y}^{m},\left(\mathbf{p}^{m}+\mathbf{q}^{m}\right)\right)+\lambda_{1}\|\mathbf{P}\|_{1, \infty}+\lambda_{2}\|\mathbf{Q}\|_{1}

    其中，

    • P=[p1⋯pM]∈RD×M\mathbf{P} = [\mathbf{p}^1 \cdots \mathbf{p}^{M}] \in \R^{D \times M} 是组稀疏分量
    • Q=[q1⋯qM]∈RD×M\mathbf{Q} = [\mathbf{q}^1 \cdots \mathbf{q}^M] \in \R^{D \times M} 是元素级稀疏分量
    • λ1\lambda_1 控制 P\mathbf P 上的组稀疏性正则化
    • λ2\lambda_2 控制 Q\mathbf Q 上的稀疏性正则化

    通俗的说，通过组稀疏分量鼓励所有任务选择同一组特征，而每个单独的任务仍可以选择与其他任务不共有的特征

  2. 鲁棒的多任务特征学习
    不仅为 W\mathbf{W} 添加行稀疏性，以选择跨任务的通用特征，还添加列稀疏性以识别与其他任务不具有相同结构的异常任务。

    通过 W=P+Q\mathbf{W} = \mathbf{P} + \mathbf{Q} 并分别对 P\mathbf{P} 和QT\mathbf{Q}^T 使用 l2,1-norm\mathcal{l}_{2,1} \text{-norm} 可以实现：

    min⁡P,Q∑m=1ML(Xm,ym,(pm+qm))+λ1∥P∥2,1+λ2∥Q∥2,1\min _{\mathbf{P}, \mathbf{Q}} \sum_{m=1}^{M} L\left(\mathbf{X}^{m}, \mathbf{y}^{m},\left(\mathbf{p}^{m}+\mathbf{q}^{m}\right)\right)+\lambda_{1}\|\mathbf{P}\|_{2, 1}+\lambda_{2}\|\mathbf{Q}\|_{2, 1}

  3. 稀疏模型与低秩模型的混合
    假设所有模型共享公共的低维子空间过于严格。为了能够同时学习不连贯的稀疏和低秩模式，将任务模型 W\mathbf{W} 分解为两个分量，即稀疏分量 P\mathbf{P} 和低秩分量 Q\mathbf{Q}：

    min⁡W,P,Q∑m=1ML(Xm,ym,wm)+λ1∥P∥1, s.t. W=P+Q,∥Q∥∗≤λ2\min _{\mathbf{W}, \mathbf{P}, \mathbf{Q}} \sum_{m=1}^{M} L\left(\mathbf{X}^{m}, \mathbf{y}^{m},\mathbf{w}^{m}\right)+\lambda_{1}\|\mathbf{P}\|_{1},\space \text{s.t.} \space \mathbf{W} = \mathbf{P} + \mathbf{Q}, \|\mathbf{Q}\|_* \le \lambda_2

    其中，

    • λ1\lambda_1 控制 稀疏分量 P\mathbf P 的稀疏性
    • λ2\lambda_2 控制 Q\mathbf Q 的秩

MTL with W=BA\mathbf{W} = \mathbf{BA}

  1. 多任务特征转换

先将原始特征转换到另一个特征空间，可以增强不同任务之间的关联，并学习不同任务之间的共享表示。一个具有特征变换的 MTL 公式化示例如下：

min⁡A,B∑m=1ML(Xm,ym,Bam)+λ∥A∥2,1, s.t. BTB=I\min _{\mathbf{A}, \mathbf{B}} \sum_{m=1}^{M} L\left(\mathbf{X}^{m}, \mathbf{y}^{m},\mathbf{Ba}^{m}\right)+\lambda\|\mathbf{A}\|_{2, 1},\space \text{s.t.} \space \mathbf{B}^T \mathbf{B} = \mathbf{I}

其中，

  • W=BA\mathbf{W} = \mathbf{BA}
  • B∈RD×D\mathbf{B} \in \R^{D \times D} 是正交变换矩阵
  • am∈RD×1\mathbf{a}^m \in \R^{D \times 1} 是特征变换后第 mm 个任务的模型参数
  • A=[a1⋯aM]∈RD×1\mathbf{A} = \left[\mathbf{a}^1 \cdots \mathbf{a}^M\right] \in \R^{D \times 1} 是对所有任务作行稀疏约束（通过 l2,1-norm\mathcal{l}_{2, 1} \text{-norm}）得到的预测矩阵

pass

  1. 多任务稀疏编码

pass

  1. 多任务低秩结构

pass

  1. 非关联任务的共享表示

pass

MTL with W=P+BA\mathbf{W} = \mathbf{P} + \mathbf{BA}

pass

不完全数据的 MTL

pass

深度学习 MTL

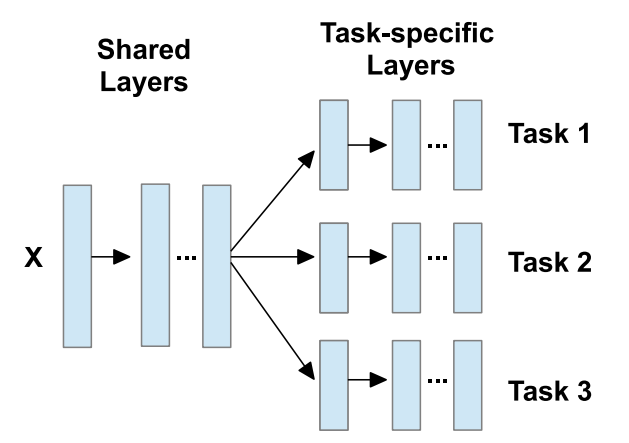
典型多任务

多任务深度学习通常有两种类型的隐藏层，

  • 共享层 学习数据的固有低秩表示，所有任务通用
  • 任务特定层 将已学习的潜在表示从先前共享层映射到任务特定的输出层

Fang et al. 提出的动态的多任务卷积神经网络（DMT CNN），每个任务都拥有一个子网，并且子网（或任务）之间共享的信息程度是灵活的。

Ranjan et al. 提出的深度多任务学习框架，可以同时进行面部检测，界标定位，姿势估计和性别识别。

Fan et al. 提出的用于大规模视觉识别的深度多任务学习算法，可以识别上万个对象类别。

Wachinger et al. 设计了一种基于3D CNN的分割算法，通过共同学习抽象特征表示和多类分类，从T1加权磁共振图像中分割出神经解剖结构。

Moeskops et al. 提出了一种基于CNN的深度学习算法，用于不同的分割任务，包括脑MRI，乳腺MRI和心脏CT血管造影（CTA）。

还有一种特殊类型的不使用共享层的深度神经网络，即网络参数不直接在任务之间共享，而是通过对不同任务的网络参数进行正则化，来共享任务之间的信息。