多任务学习
问题陈述
符号说明
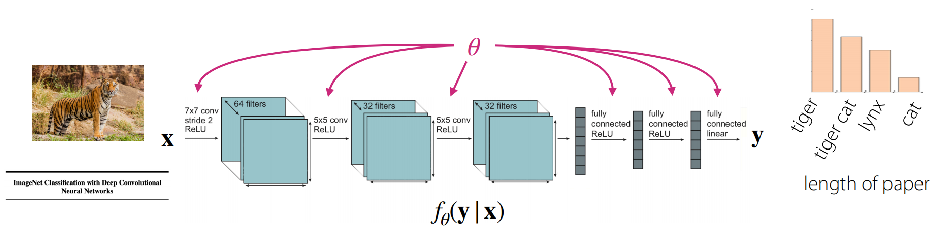
-
单任务学习
数据集: D={(x,y)k}
目标: minθL(θ,D)
典型损失函数-负对数似然:L(θ,D)=−E(x,y)∼D[logfθ(y∣x)]
-
任务
任务的形式化定义:Ti≜{pi(x),pi(y∣x),Li},其中,pi 为数据生成的分布
对应数据集;Ditr,Ditest,其中将 Ditr 计为 Di
基本设置
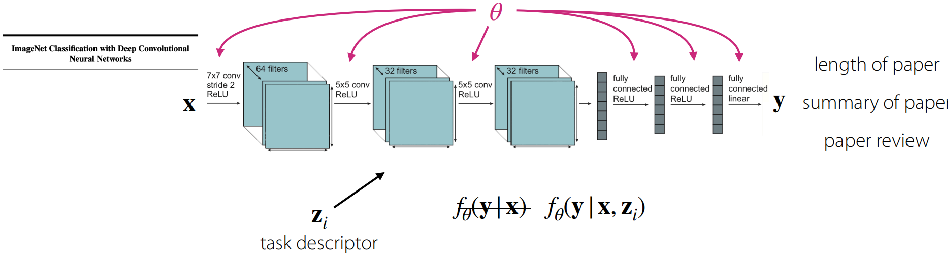
MTL 目标:minθ∑i=1TLi(θ,Di)
模型,目标,优化
模型
任务的训练
-
两种极端情况
-
使用独立的网络对每个任务单独进行训练,不共享参数
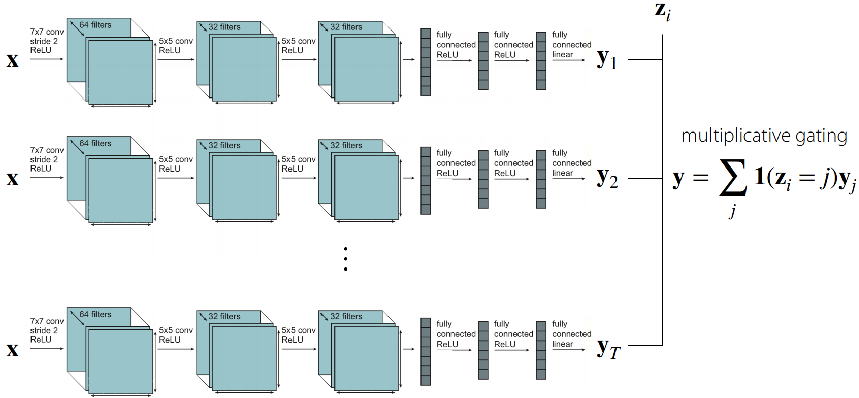
-
将 zi 的输入或激活层连接起来,共享全部参数
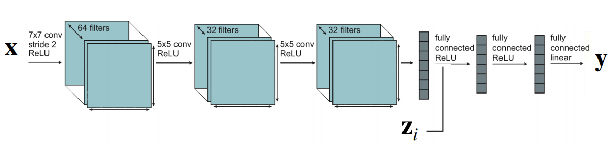
-
折衷 MTL 架构
将 θ 拆分为共享参数 θsh 和任务特定参数 θi,从而 MTL 的目标为:
θsin,θ1,…,θTmini=1∑TLi({θsh,θi},Di)
任务特定参数对其特定的任务进行优化;共享参数对所有任务进行优化。
选择如何训练任务 zi 等效于 选择如何/在哪里共享参数。
通用设置
-
基于串联
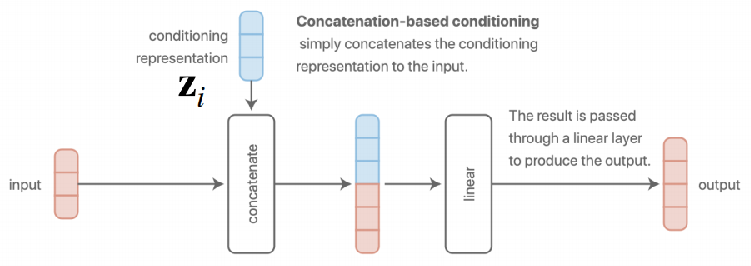
简单地连接特征表示作为输入,送入一个线性层来产生输出层。
-
基于附加
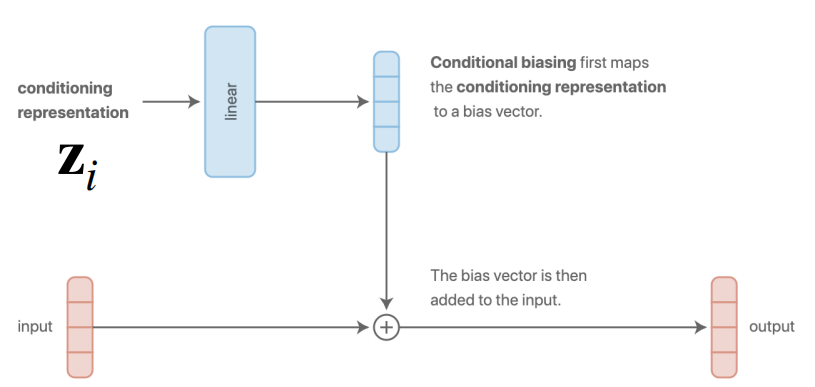
先将特征表示映射到偏置向量,再将偏置向量添加到输入。
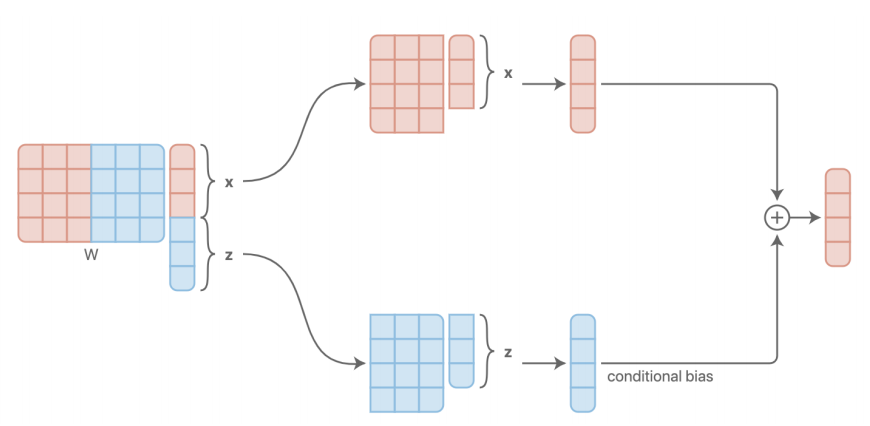
基于串联或附加的方法实际上是等效的
-
多头架构
-
基于乘积
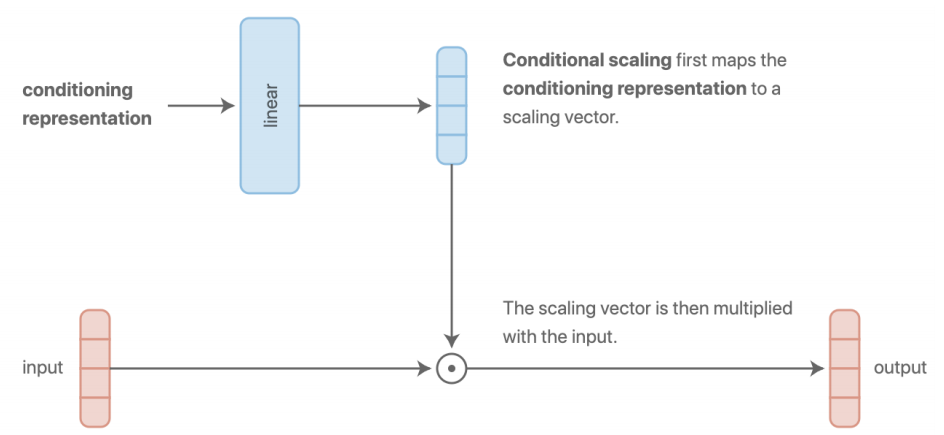
类似于附加的方法,将特征表示映射到 scaling 向量,再与输入相乘。
它在每一层都更具表现力,并且使用乘法门也非常自然,它更加一般化.
-
更复杂的设置
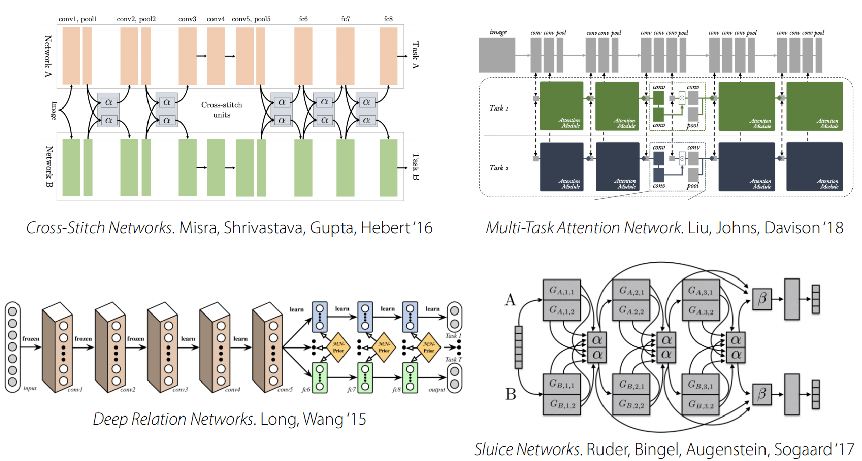
这些方法目前还是具有一些缺陷:
目标
θmini=1∑TLi(θ,Di)
通常对任务赋予不同权值:
θmini=1∑TωiLi(θ,Di)
优化
步骤
- 对任务进行小批量采样 B∼{Ti}
- 对每个任务小批量采样数据点 Dib∼Di
- 计算小批量的损失 L^(θ,β)=∑T∈βLk(θ,Dkb)
- 反向传播损失以计算梯度 ΔθL^
- 将梯度应用于合适的神经网络优化器(例如,Adam)
注意
- 该流程确保无论数据量如何,均可以对任务进行统一的采样
- 对于回归问题,需要确保任务标签的大小相同
挑战
负向迁移
在某些情况下,独立的网络更优,如:

原因
- 优化挑战:跨任务干扰,任务学习速率不同
- 可表示性有限:多任务学习通常需要更大的网络
解决方案
θ5,θ1,…,θTmini=1∑TLi({θsh,θi},Di)+t=1∑T∥∥∥θt−θt′∥∥∥
这里, ∑t=1T∥∥∥θt−θt′∥∥∥ 是软参数共享,它可以平滑地约束两个网络之间的权重,允许参数共享的程度非常灵活:
- 若该值限定为 0,则任务之间不共享参数;
- 若该值限定非常大,则类似于硬参数共享;
然而这样会带来新的超参数,需要对其进行优化。
过拟合
原因:共享不足
解决方案:共享更多信息,形成更加强的规则形式
迁移学习
多任务学习 VS 迁移学习
| 多任务学习 |
迁移学习 |
| 同时解决多个任务 T1,⋯,TT |
在解决源任务 Ta 后,将从任务 Ta 所学的知识迁移,从而解决目标任务 Tb |
关键假设:迁移过程中不能访问数据 Da
注:任务 Ta 本身可能包含多个任务
迁移学习是多任务学习的一个有效解决方案,但反之则不然。
通过微调进行迁移学习
ϕ←θ−αΔθL(θ,Dtr)
其中,
- Dtr 是新任务的训练数据
- θ 是预训练参数
如何获取预训练参数
- ImageNet 分类
- 在大型语料库(如BERT,LMs)上训练的模型
- 其他无监督学习技术
- 任何大型的多样化数据集
通用实践方法
- 以较小的学习速率进行微调
- 为靠前的层赋予较小的学习速率
- 冻结较靠前的层,并逐渐解冻
- 重新初始化最后一层
- 通过交叉值搜索超参数
- 架构选择(如,ResNets)

















